Cześć. Dziś nieco bardziej matematycznie.
Szybka powtórka: Całka to pole powierzchni pod wykresem funkcji.
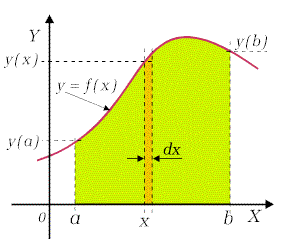
Całka oznaczona na przedziale <a,b></a,b>
Wartość całki jest t więc pole powierzchni tej zielonej figury.
Słowem wstepu.. Mamy 4 popularne metody numeryczne które pozwalają obliczyć wartość całki:
- Metoda prostokątów – pole powierzchni przybliżane jest poprzez podzielenie obszaru na prostokąty.
- Metoda trapezów – pole powierzchni przybliżane jest poprzez podzielenie obszaru na trapezy.
- Metoda Monte Carlo – zliczamy punkty które wpadają w wykres funkcji.
- Metoda Simpsona – będziemy obliczali sumy wycinków obszarów pod parabolą.
Dziś zajmiemy się metodą która jest najlepsza biorąc pod uwagę skomplikowanie i dokładność – czyli metodę trapezów. Dokładniejsza od niej jest metoda Simpsona, ale jest nieco bardziej skomplikowana.
Ok, skoro wiemy że będziemy sumować sumy pól powierzchni trapezów to warto przypomnieć wzór na pole trapezu:
![]() .
.
Dzielimy teraz pole powierzchni na n trapezów. Wysokość każdego z trapezów będzie taka sama i będzie równa
![]()
Teraz musimy wyznaczyć punkty, czyli przedział dzieli na n równych partii wzorem:
![]()
No i teraz wystarczy zsumować pola, które, wg wzoru pierwszego to:
![]()
Więc mamy taką sumę:
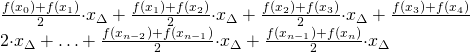
No to wyciągamy przed nawias
![]()
i dostajemy:
![]()
I po przekształceniach dostajemy wzór na całkę:
![]()
No i dostaliśmy finalną wersję wzoru iteracyjnego na obliczenie wartości całki w metodzie trapezów.
Teraz przystąpny do implementacji. Funkcję którą bedziemy całkować stworzyłem jako metodę klasy abstrakcyjnej. Klasa która liczy całkę rozszerza klase z funkcją co daje nieco wygody.. Ok, pierw wywołanie:
1 2 3 4 5 6 7 8 9 | public class Calka { public static void main(String[] args) { Integral i = new Integral(100000, 0, 5); System.out.println(i.calc()); } } |
Jak widzimy w kodzie, funkcja którą bedziemy całkować to funkcja kwadratowa. W konstruktorze pierw podziejmy dokładność operacji (im większe tym wolniej i dokładniej) no i odpowiednio – a i b – przedziały całkowania. Tutaj obliczamy całkę taką:
![]()
No i klasa Integral:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | public class Integral { double dokladnosc; double xp; double xk; double dx; public Integral(double n, double xp, double xk) { this.xk = xk; this.xp = xp; this.dokladnosc = n; dx = (xk - xp) / n; } private double f(double x) { return (x * x); } public double calc() { double wynik = 0; for (double i = 1; i < dokladnosc - 1; i++) { wynik = wynik + f(xp + i * dx); } wynik = (wynik + ((f(xp) - f(xk) / 2))) * dx; return wynik; } } |
Na koniec porównanie wyników:
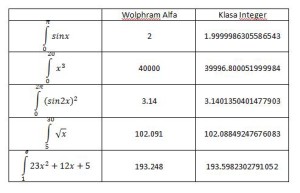
Myślę że dokładność jest wystarczająco dobra przy dokładności podaje w konstruktorze równej 100000. Jeśli jest potrzeba – można zwiększyć.
Mateusz Mazurek






