Kolejna rzecz z algorytmiki.
Kopce :)
Kopiec to takie drzewo binarne w którym:
- Wartość klucza (czyli wartość po prostu) w każdym węźle jest nie mniejsza/nie większa niż u jego potomków.
- Wszystkie liście leżą na co najwyżej dwóch sąsiednich poziomach.
- Liście na ostatnim poziomie szczelnie wypełniają lewą część drzewa.
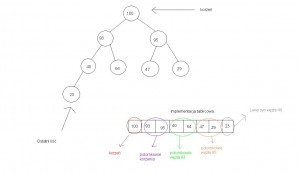
Kopiec to taka struktura której implementacją może byc zwykły wektor (tablica jednowymiarowa). Przykład kopca i jego implementacja tablicowa:
Kliknij aby powiększyć.
Ok, to w miare przybliżyłem istotę kopca. Warto pamiętać że kopiec jest drzewem binarnym. Nazwaliśmy najważniejsze węzły w kopcu, to teraz, aby w pełni zrozumieć istotę sortowania przez kopcowanie omówię przywracanie własności kopca.
Czasem, w skutek jakis operacji, kopiec traci własności kopca. Najczęściej jest to własność mówiąca o wartościach, że muszą one się sukcesywnie, poziomami, zmniejszać.
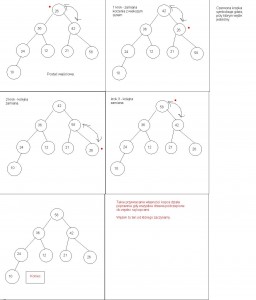
Zaczynamy rekurencyjnie przeglądać kopiec, od korzenia w dół. Szukamy większego z potomków korzenia i w tę drogę się kierujemy. Jeśli syn korzenia jest większy niż korzeń to zamieniamy go. Z węzłem na drugim poziomie również robimy to samo, wybieramy większego z synów i jesli jest wiekszy od ojca to zamieniamy :) Popatrz na przykład:
Kliknij aby powiększyć.
No dobra, to przejdźmy do sedna…
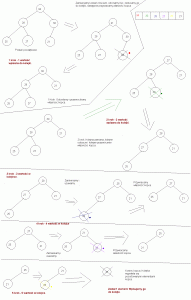
Sortowanie przez kopcowanie polega na cyklicznej wymianie liścia z korzniem, odcinaniu liścia i przywróceniu własności kopca. Odcinane liście umieszkane są w kolejce. Pokażę jak to wygląda na jakimś kopcu:
Koniecznie kliknij aby powiększyć.
Sortowanie to, ma złożoność obliczeniową O(nlg(n)). Wynika to z tego, że czas przywracania własności kopca jest O(lg(n)).
Mateusz Mazurek