Cześć! W tej cześci odejdziemy nieco od naszej klasy Czlowiek :) Poznamy rekurencję oraz pokaże przykład działania zmiennych statycznych a przy okazji złapiemy mały expieriance w temacie Algorytmów. Pokaże też subklasy.
Ok, słowem wstępu opowiem Wam co będziemy implementować. Jakiś czas temu wyyślono coś takiego jak struktury danych. O niektórych już pisałem na tym blogu – chociażby lista. Dla k-tego elemntu listy trzeba zrobić k kroków. Co, wbrew logice, jest kiepskim wynikiem. Bo jak mamy 1000 elementów w liście to żeby dojść do 900 elementu musimy zrobić 900 przesuwań wskaźnika.. Very bad. No, może nie very, ale nadal bad.
Lista ma zawsze jakiś następny element – jest nim kolejlny element lub null – czyli znak że jest koniec listy.
Liczby można przetrzymywać sprytniej :) Takim sposobem są Drzewa Przeszukiwań Binarnych ;) Nie bez powodu wstawiłem ten link tu. Kliknij w niego i zobacz co to jest.
BEZ TEGO NIE IDŹ DALEJ.
Popatrzyłeś? Ok, to możemy iść dalej.
Od strony implementacji jeden węzeł drzew, czyli jedno takie kółko z wartością w środku będzie wyglądało tak:
1 2 3 4 5 6 7 8 9 10 | private class Node{ int val; // wartosc Node left; // referencja do lewego dziecka Node right; // referencja do prawego dziecka int key; //klucz Node parent; // referencja do rodzica Node(int a){ this.val=a;} // konstruktor } |
Każdy węzeł będzie obiektem wewnętrznej prywatnej (lub chronionej – zależnie czy mamy w planach dziedziczyć) klasy Node.
Ważnym elementem, który czyni drzewa binarnym ciekawą strukturą danych (a przy okazji prostą) jest możliwość cwanego przeszukiwania ich wykorzystując zależności wyboru poddrzewa dla kolejnego elementu.
Ale to będę tłumaczył już przy samej implementacji.
Ok, to zaczynamy!
Stwórzmy węzeł sobie który będzie zawsze wskazywał na korzeń drzewa, czyli pierwszą wartość dodaną do drzewa oraz zmienną statyczną.. Co ona będzie robić? Na razie to mało istotne, ale to jak działa jest już całkiem ważne – zmienne statyczne nie tracą swojej wartości w obrębie jednego kontenera (funkcji, klasy itp). Czyli jeżeli stworzymy obiekt klasy i zrobimy jakieś operacje na tej zmiennej to będzie ona miała wartość zmienioną a nie początkową.. Rozumiesz? Jeśli tak to fajnie, jeśli nie, to poczekaj, zrozumiesz.
1 2 | Node root; static int key=1; |
Nasza klasa będzie nazywać sie BST. Tworzymy konstruktor
1 2 3 4 5 6 | public BST(int v){ root= new Node(v); // 1 root.key=1; // 2 root.parent=null;// 3 } |
1. Tworzymy nowy obiekt wewnętrznej klasy (tzn. subklasy) i przypisujemy go do zmiennej root.
2. Ustawiamy key na 1, gdyż będzie to nasz pierwszy element drzewa – korzeń.
3. Skoro to korzeń to jako jedyny element w drzewie – nie ma rodzica.
Teraz chyba najtrudniesza rzecz do napisania.. Oczywiscie z tych które przygotowałem na tę lekcję. Napiszmy metodę która będzie umieszczała wartość podaną przez użytkownika w ODPOWIEDNIM miejscu drzewa. Czyli ma wyszukać takie miejsce w drzewie żeby zachować właściwość drzewa BST. Mam na myśli oczywiście to że po lewej stronie do węzła są wartości mniejsze a po prawej większe.
Algorytm:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | 1. Pobierz wartość nowego węzła. 2. Stwórz węzeł w tą wartością. 3. current <= root -- Pętla -- 4. Jeśli wartosć current jest mniesza od dodawanej.. 5. Sprawdź czy prawe dziecko current jest nullem (jest wolny) 6. Jeśli tak to podczepiamy stworzony węzeł jako prawe dziecko currenta i wychodzimy z pętli (przejście do 12 pkt) 7. Jeśli nie to przesuwamy current w prawo. 8. Jeśli current NIE jest mniejsze od dodawanej.. 9. Sprawdź czy lewe dziecko current jest nullem (jest wolny) 10. Jeśli tak to podczepiamy stworzony węzeł pod lewe dziecko currenta i wychodzimy z pętli (przejście do 12 pkt) 11. Jeśli nie to przesuwamy current w lewo. -- Koniec pętli -- 12. Koniec. |
Mimo że średnio to wygląda – jest proste. Zrobię przykład. Do takiego drzewa:

I chcemy dodać liczbę 8 :)
Krok po kroku jak będzie przebiegał algorytm. Kroki zaznaczane są czerwoną strzałką.
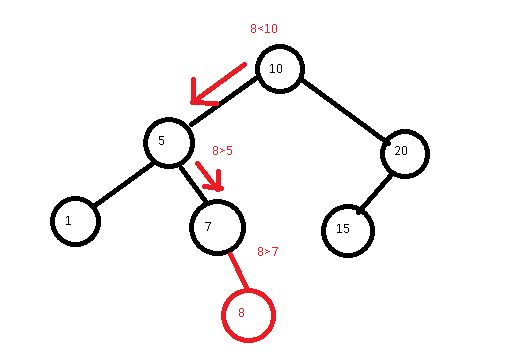
Mam nadzieje że już rozumiesz. Teraz czas na kod :) Kroki algorytmu jako komentarze.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 | public boolean addNode(int v){//1 this.key++;//2 Node n = new Node(v);//2 n.key=this.key;//2 Node current=root;//3 while(true){ if(current.val<v){//4 if(current.right==null){//5 n.parent=current;//6 current.right=n;//6 break;//6 }else{ current=current.right;//7 } }else{//8 if(current.left==null){//9 n.parent=current;//10 current.left=n;//10 break;//10 }else{ current=current.left;//11 } } } return true;//12 } |
Dopiszmy teraz coś co wyświetli nam wartości drzewa. Mamy do wyboru 3 algorytmy:
PostOrder
PreOrder
InOrder
Ja wybrałem PreOrder. Czym one się różnią? W sumie każde z nich jest REKURENCYJNYM sposobem przechodzenia drzewa, różnią się co do kolejności odwiedzania wierzchołków.
żeby zrozumieć rekurencję, trzeba zrozumieć rekurencję ;) musiałem to napisać. Popatrzmy na kod dwóch metod:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | private void show(Node a){ System.out.println(a.val); if(a.left!=null) show(a.left); if(a.right!=null) show(a.right); } public void showAll(){ this.show(root); } |
Metoda publiczna to kontener dla metody prywatnej (opakowanie jej, nic skomplikowanego). Do metory prywatnej przekazujemy roota, czyli nasz korzeń. Metoda show() wyświetla wartość korzenia potem sprawdza czy ma lewe dziecko, jesli tak, to wywołuje siebie samą.. Może, przecież jest zdefiniowana. Funkcja który wywołuje jest zawieszona i czeka na zakończenie funkcji którą wywołała. Więc wchodzmy z a.left do show() – wyświetla ten węzeł i znów sprawdza i znów wchodzi.. I tak dalej.. Jaki efekt? Efekt algorytmu z powrotami – czyli rekurencja się cofnie w pewnym momencie i zacznie przechodzić do drugiego ifa = wyświetlac prawe poddrzewo :) Rekurencja jest mało efektywna w niektórych zastosowaniach. Ale każdą rekurencyjną implementację można zapisać w postaci iteracyjnej.
Czy widzisz może już zastosowania takiego drzewa? Popatrz na te funkcje i pomyśl jak duży zysk efektywności jest w porównaniu co do np. wcześniej wspomnianej listy:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | public int getMax(){ Node t= root; while(t.right != null) t=t.right; return t.val; } public int getMin(){ Node t= root; while(t.left != null) t=t.left; return t.val; } |
Nawet przy średnio zrównoważonych drzewach wyszukiwanie największych/najmniejszych wartości jest bardzo szybkie. Zdecydowanie szybsze niż naiwne wyszukiwanie w tablicy czy w liście. W najgorszym możliwym przypadku (drzewo pochylone) czas jest porównywalny z listą.
Co znaczy że drzewo jest zrównoważone? Chodzi o to że wartości można tak ustawić żeby było ono jak najmniejsze. A co z tym idzie – przeszukiwanie jak najszybsze. Przeprowadźmy test..
Przy okazji zobaczycie jak w łatwy sposób mierzyć czas wykonywania się fragmentu kodu. Sprawdźmy czas wyszukiwania największego elementu w 100 elemenowym zbiorze liczb mniejszych od 1000 generowanych „losowo”. Wprowadzimy te same liczby do drzewa, do listy i do tablicy. Popatrz na kod:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 | /* * To change this template, choose Tools | Templates * and open the template in the editor. */ package pro; import java.util.ArrayList; import java.util.Iterator; import java.util.List; import java.util.ListIterator; import java.util.Random; /** * * @author Matt */ public class Pro { /** * @param args the command line arguments */ public static void main(String[] args) { Random r = new Random(); BST f=null; //referencja do drzewa int i=0;// zmienna iterujaca int tablica[] = new int[100];//tablica 100 elementow List lista = new ArrayList (100); //lista 100 elementow while(i<100) //wypelniamy 3 struktury danych na raz { int t = r.nextInt(1000);//losuje liczbe tablica[i]= t;//wpisuje do tablicy lista.add(t); //dodaje do listy if(f==null) { f=new BST(t); } else { f.addNode(t);//wypelniam drzewo } i++; } //==================================================== //==================================================== //==================================================== long start=System.nanoTime(); // czas staru pomiaru int m=f.getMax(); //szukam w drzewie maxa long stop=System.nanoTime();//czas zakonczenia pomiaru System.out.println("Max dla drzewa: "+m);//wyswietlam max znaleziony w drzewie System.out.println("Czas wykonania w ns dla drzewa:"+(stop-start));//roznica w czasach to czas wykonania //======================== //======================== //======================== int max=0;//max poczatkowy long start1=System.nanoTime();// for(i=0;i<100;i++){ if(tablica[i]>max) max=tablica[i]; //iteracyjnie, naiwnie szukam maxa w tablicy } long stop1=System.nanoTime(); System.out.println("Max dla tablcy: "+max); System.out.println("Czas wykonania w ns dla tablicy:"+(stop1-start1));//licze drugi czas wynokania //======================== //======================== //======================== int max2=0; long start2=System.nanoTime(); for(i=0;i<100;i++){ if(lista.get(i) >max2) max2=lista.get(i);//dla listy } long stop2=System.nanoTime(); System.out.println("Max dla listy: "+max2); System.out.println("Czas wykonania w ns dla listy:"+(stop2-start2)); //teraz wstawiam czasy wykonywania sie do tablicy long a[]= new long[3]; a[0]=stop-start; a[1]=stop1-start1; a[2]=stop2-start2; //szukan najmniejszej różnicy long naj=a[0]; for(i=1;i<3;i++){ if(a[i]<naj) naj=a[i]; } //i wyswietlam co wygrało wyścig if(naj==a[0]) System.out.println("Najszybciej drzewo"); if(naj==a[1]) System.out.println("Najszybciej tablica"); if(naj==a[2]) System.out.println("Najszybciej lista"); } } |
Dla 10 uruchomień wyniki przedstawiają się tak:
|
[ns] |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Drzewo | 4562 | 3992 | 3993 | 4563 | 5133 | 4562 | 14828 | 5132 | 4564 | 4563 |
| Tablica | 6273 | 5703 | 5703 | 6843 | 6273 | 6843 | 6844 | 5703 | 5703 | 5133 |
| Lista | 48474 | 37640 | 52467 | 38780 | 40491 | 271459 | 50756 | 38210 | 36499 | 37069 |
Wyniki nie są zaskakujące. Pogrubiłem strukturę która była w danej próbie najszybsza. Zapytacie.. Co się stało w próbie 7? Sprawdopodobnie napływ danych był tak pesymistyczny, że drzewo było mniej zrównoważone niż w poprzednich próbach.
Zobaczmy jak przedstawia się taka tabela gdy ilość liczb pomnożymy przez 100.
|
[ns] |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Drzewo | 13828 | 25093 | 11406 | 17109 | 12547 | 19960 | 29085 | 25093 | 22241 | 27374 |
| Tablica | 852017 | 910187 | 1477628 | 710014 | 820081 | 483608 | 1421739 | 3449699 | 613064 | 7364758 |
| Lista | 3599117 | 3656145 | 4705484 | 4191650 | 3649827 | 3797297 | 3847193 | 7993220 | 7290834 | 1868279 |
Tutaj bezsprzecznie wygrywa drzewo.
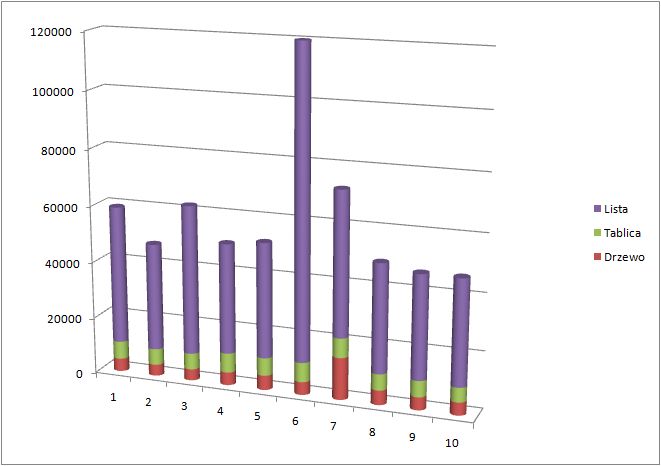
Może bardziej przemawiać będą wykresy:
Wykres dla 100 wartości.
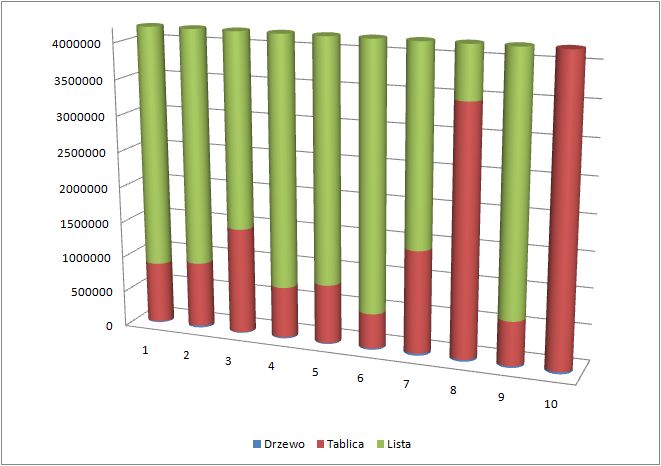
Oraz wykres dla 10000 wartości:
Nie trzeba być super inżynierem żeby mieć pewnosć że nawet średno zrównoważone drzewo będzie szybsze przy szukaniu najwiekszej wartości niż lista i tablica. Drzewo równoważy się poprzez rotacje w prawo i w lewo. Ale o tym kiedy indziej.
Skąd taka rozbieżność między tablicą i listą? Lista traci sporo czasu na dostęp do n-tego elementu, kiedy dostęp do elementów tablicy wykonuje się w czasie stałym.
Uff, ta częśc kursu pokazała Javę od nieco algorytmicznej strony.. Ale to nie jest złe. Zobaczyłeś że klasa w klasie nie jest zła, a zmienne statyczne.. Moga być użyteczne… Właśnie. Umiałbyś przerobić klasę BST tak zeby używała pola key? :)
Mateusz Mazurek