Mateusz Mazurek – programista z pasją

Python, architektura, ciekawostki ze świata IT

    • Algorytmika Programowanie

    Algorytmy genetyczne w Pythonie – ciąg dalszy

    Mateusz M. Opublikowane w
    🕑 6 minuty czytania

    W jednym z ostatnich wpisów omówiliśmy, czym jest algorytm genetyczny, z czego się składa i na czym polega jego działanie. Napisaliśmy również mini framework, ułatwiający pracę z tym rozwiązaniem, aby na końcu, w oparciu o nasz poprzedni kod, stworzyć przykład, który pozwala przekształcić losowy ciąg znaków w zadany tekst. Zrobiliśmy tam naprawdę dużo! Jeśli nie czytałeś poprzedniego wpisu, zachęcam do nadrobienia zaległości, link załączam tutaj.

    Przykład, który pokazałem w poprzednim artykule, chociaż ciekawy, to nie rozwiązuje żadnego konkretnego problemu. Zatem, aby AI nie było tutaj tylko buzzwordem, dziś zajmiemy się konkretnym zadaniem.

    Problem komiwojażera

    Zajmiemy się problemem, z którym na co dzień borykają się chociażby firmy kurierskie. W szczególności teraz, pod koniec roku, kiedy wszyscy zamawiamy prezenty. Ilość paczek, które trzeba dostarczyć jest ogromna i żeby dokonać tego w rozsądnym czasie, trzeba zaplanować trasę, którą kurier ma jechać.

    I to właśnie problem wyznaczenia optymalnej trasy jest nazywany problemem komiwojażera.

    Z perspektywy matematyka

    Problem ten z perspektywy matematyki to problem z dziedziny grafów. Zbudować należy graf ważony, którego wierzchołki są miastami. Najpierw każdą parę miast łączymy krawędziami. Następnie każdej krawędzi nadajemy wagę równą odległości miedzy odpowiednimi miastami.

    obrazek
    Przykładowy graf (bez wag) dla 10 miast.

    Istnieją dwie odmiany tego problemu. Symetryczny problem komiwojażera (STSP) polega na tym, że dla dowolnych miast A i B odległość z A do B jest taka sama jak z B do A. W asymetrycznym problemie komiwojażera (ATSP) odległości te mogą być różne. My rozważamy pierwszą odmianę.

    Otrzymujemy w ten sposób graf pełny, który ma tyle wierzchołków, ile miast musi odwiedzić komiwojażer (wliczając w to miasto, z którego wyrusza). Odwiedzenie wszystkich miast odpowiada cyklowi, który przechodzi przez każdy wierzchołek danego grafu dokładnie raz. Cykl taki nazywamy cyklem Hamiltona. Poszukujemy wiec w grafie pełnym cyklu Hamiltona o minimalnej sumie wag krawędzi.

    Rozwiązanie naiwne

    Pierwsze rozwiązanie, które przychodzi na myśl, to oczywiście wyznaczyć wszystkie możliwe drogi, obliczyć ich długości i wybrać najkrótszą.

    Głównym problemem tego rozwiązania jest ilość danych, które trzeba przetworzyć. Zakładając, że rozważamy symetryczną odmianę tego problemu, ilość możliwych kombinacji wynosi

    \frac{(n-1)!}{2}

    co dla zaledwie 20 miast (lub po prostu konkretnych punktów na mapie) daje

    \frac{19!}{2} \approx 6 \cdot 10^{16}

    możliwych kombinacji. Sporo! Komputer może się nieźle napocić. A co, jeśli punktów do przejechania mamy sto?

    Rozwiązania przybliżone

    Jak już pewnie zauważyliście, okazuje się, że rozwiązanie tego problemu nie jest trywialne. W związku z tym akceptowalne są rozwiązania przybliżone, czyli po prostu bliskie najlepszemu, ale nie najlepsze. Akceptując niedoskonałość, potrafimy rozwiązać ten problem właśnie z użyciem algorytmów genetycznych!

    Kod

    Napiszmy więc kawałek kodu, dzięki któremu rozwiążemy problem komiwojażera. Użyjemy do tego naszego mini AI framework’a, czyli zaimplementujmy klasę Element:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    from genetic_library import GeneticAlgorithm, Element
    from genetic_library.selection_models import elite_selection_model

    from random import randint, sample
    from math import sqrt

    START_POINT = [(1, 1)]
    END_POINT = [(1, 1)]
    # POINTS = [(randint(0, 40), randint(0, 40)) for k in range(50)]
    POINTS = [(3, 4), (11, 5), (27, 23), (27, 25), (22, 32), (24, 34), (19, 38), (17, 37), (7, 40), (8, 36),
              (8, 28), (16, 21), (14, 17), (25, 11), (24, 19), (32, 26), (29, 34), (27, 34), (38, 36), (35, 12), (33, 8),
              (31, 2), (24, 5), (23, 3), (17, 3), (16, 3), (24, 11), (21, 21), (23, 21), (17, 10), (19, 7), (33, 14),
              (38, 18), (34, 19), (20, 30), (9, 38), (6, 27), (7, 12), (3, 15), (0, 24), (5, 30), (3, 33), (4, 33),
              (6, 28), (7, 6), (4, 4), (2, 10), (2, 23), (8, 20)]


    class Route(Element):
        def __init__(self, points):
            self.points = points
            super().__init__()

        def _perform_mutation(self):
            first = randint(1, len(self.points) - 2)
            second = randint(1, len(self.points) - 2)

            self.points[first], self.points[second] = self.points[second], self.points[first]

        def crossover(self, element2: 'Element') -> 'Element':
            child_points = self.points[1:int(len(self.points) / 2)]
            for point in element2.points:
                if point not in child_points and point not in END_POINT + START_POINT:
                    child_points.append(point)

                if len(child_points) == len(element2.points):
                    break
            return Route(START_POINT + child_points + END_POINT)

        def evaluate_function(self):
            def _calculate_distance(x1, x2, y1, y2):
                return sqrt((x2 - x1) ** 2 + (y2 - y1) ** 2)

            sum = 0
            for i, p in enumerate(self.points):
                if i + 1 > len(self.points) - 1:
                    break
                next_point = self.points[i + 1]
                sum += _calculate_distance(p[0], next_point[0], p[1], next_point[1])

            return sum

        def __repr__(self):
            return str(self.points)


    def first_generation_generator():
        return [Route(START_POINT + sample(POINTS, len(POINTS)) + END_POINT) for _ in range(100)]


    def stop_condition(string, current_fitness, i):
        return i == 3000


    ga = GeneticAlgorithm(first_generation_generator, elite_selection_model, stop_condition)
    ga.run()

    Zaczynając od samej góry, najpierw definiujemy punkt będący jednocześnie punktem początkowym jak i końcowym. Lista POINTS to po prostu koordynaty naszych miast do odwiedzenia. Zajmijmy się opisanymi w poprzednim artykule metodami, zaczynając od mutacji:

    1
    2
    3
    4
    5
        def _perform_mutation(self):
            first = randint(1, len(self.points) - 2)
            second = randint(1, len(self.points) - 2)

            self.points[first], self.points[second] = self.points[second], self.points[first]

    Jej działanie to po prostu zamiana miejscami dwóch różnych punktów na trasie. Krzyżowanie się osobników wygląda tak:

    1
    2
    3
    4
    5
    6
    7
    8
    9
        def crossover(self, element2: 'Element') -> 'Element':
            child_points = self.points[1:int(len(self.points) / 2)]
            for point in element2.points:
                if point not in child_points and point not in END_POINT + START_POINT:
                    child_points.append(point)

                if len(child_points) == len(element2.points):
                    break
            return Route(START_POINT + child_points + END_POINT)

    Polega ono na wzięciu z pierwszego osobnika (czyli możliwej drogi) części punktów jego trasy (pomijając punkt początkowy) i dobieraniu w pętli kolejnych punktów z drugiego osobnika (czyli innej możliwej drogi) tak, by się one nie powtarzały. Osiągnięcie tego celu kończy pętlę i zwraca nowego osobnika (drogę), w tym przypadku klasę Route. Dalej mamy funkcję oceny:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
        def evaluate_function(self):
            def _calculate_distance(x1, x2, y1, y2):
                return sqrt((x2 - x1) ** 2 + (y2 - y1) ** 2)

            sum = 0
            for i, p in enumerate(self.points):
                if i + 1 > len(self.points) - 1:
                    break
                next_point = self.points[i + 1]
                sum += _calculate_distance(p[0], next_point[0], p[1], next_point[1])

            return sum

    tutaj mamy prosto – liczymy odległość pomiędzy punktami

    A=(x_1,y_1), B=(x_2,y_2)

    wg wzoru:

    AB=\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}

    Czekaj, stop!

    Podoba Ci się to co tworzę? Jeśli tak to zapraszam Cię do zapisania się na newsletter:
    a w ramach prezentu otrzymasz całkowicie za darmo, dwa dokumenty PDF „6 (nie zawsze oczywistych) błędów popełnianych podczas nauki programowania” który jest jednym z efektów ponad siedmioletniej pracy i obserwacji rozwoju niejednego programisty oraz „Wstęp do testowania w Pythonie”, będący wprowadzeniem do biblioteki PyTest.
    Jeśli to Cię interesuje to zapraszam również na swoje social media.

    Jak i do ewentualnego postawienia mi kawy :)
    Postaw mi kawę na buycoffee.to

    Innymi słowy – liczymy odległość od punktu startu do pierwszego punktu. Następnie odległość między drugim a trzecim punktem i tak dalej, aż do końca listy miast z rozważanego osobnika (drogi). Uzyskane wyniki sumujemy, czyli uzyskujemy długość konkretnej drogi.

    Rezultat

    Tak jak w poprzednim artykule tak i tu każde uruchomienie programu zakończy się innym wynikiem. Z kodu wynika, że ustawiłem limit 3000 pokoleń – i to wystarczy żeby średnio z 850 jednostek długości zoptymalizować trasę do średnio 360 jednostek. Wynik ten jest dla 51 miast. Przypomnę, że generuje to wg wzoru

    \frac{(n-1)!}{2}

    około

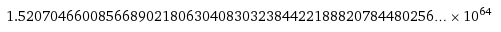
    kombinacji!! Jeśli ktoś nie jest zaznajomiony z matematycznym zapisem używającym potęgi liczby 10, czyli z notacją wykładniczą, to oto liczba kombinacji:

    15207046600856689021806304083032384422188820784480256000000000000

    Wizualizacja

    Załączam niżej wizualizację jednego uruchomienia programu. Do kodu, który jest wyżej, dopisałem kawałek matplotlib’a, który umie takie fajne rzeczy robić!

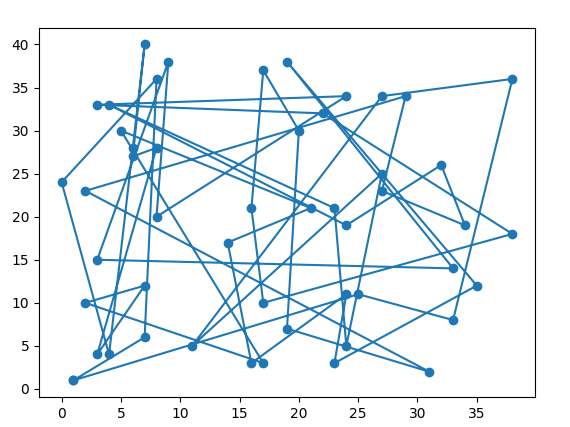
    Video pokazuje również output jaki generuje nasz framework. Filmik oczywiście jest przyśpieszony. Dla osób nie lubiących filmików załączam wynik innego uruchomienia, stan początkowy:

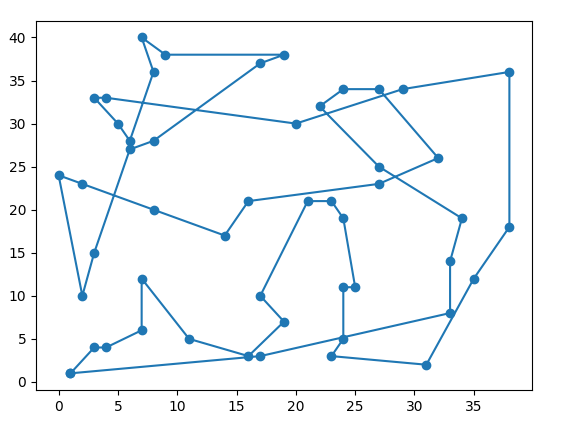
    stan po 3500 pokoleń:

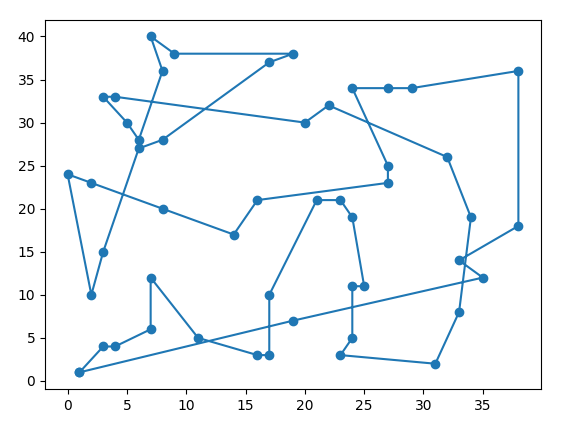
    stan po 10000 pokoleń:

    Github

    Na githubie, o którym wspomniałem w poprzednim artykule tj https://github.com/mmazurekdev/genetic-algorithm pojawiła się wersja kodu, który przygotowaliśmy w tym artykule – zarówno z generowaniem wizualizacji jak i bez.

    Dzięki za wizytę,
    Mateusz Mazurek

    A może wolisz nowości na mail?

    Podobne artykuły:

    Otagowano:
    Subskrybuj
    Powiadom o
    guest

    Witryna wykorzystuje Akismet, aby ograniczyć spam. Dowiedz się więcej jak przetwarzane są dane komentarzy.

    2 komentarzy
    Inline Feedbacks
    View all comments
    Mateusz Rus

    Jak zwykle bardzo ciekawy wpis. Problem komiwojażera to jedno z ciekawszych zagadnień w świecie IT.

    Pozdrawiam, Mateusz.

    5
    Odpowiedz