Raz na jakiś czas wchodzę chodzę sobie na stronkę Project Euler i pisze programy, rozwiązując czasem ciekawe problemy, wymyślone przez użytkowników. Pewnie nie jedna osoba powie, że to strata czasu, bo bardzo często są to zagadnienia matematyczne, nie mające dużo wspólnego z praktyczną stroną programowania.
Dziś jednak wykorzystam Problem 8, brzmiący:
Find the greatest product of five consecutive digits in the 1000-digit number.
73167176531330624919225119674426574742355349194934
96983520312774506326239578318016984801869478851843
85861560789112949495459501737958331952853208805511
12540698747158523863050715693290963295227443043557
66896648950445244523161731856403098711121722383113
62229893423380308135336276614282806444486645238749
30358907296290491560440772390713810515859307960866
70172427121883998797908792274921901699720888093776
65727333001053367881220235421809751254540594752243
52584907711670556013604839586446706324415722155397
53697817977846174064955149290862569321978468622482
83972241375657056057490261407972968652414535100474
82166370484403199890008895243450658541227588666881
16427171479924442928230863465674813919123162824586
17866458359124566529476545682848912883142607690042
24219022671055626321111109370544217506941658960408
07198403850962455444362981230987879927244284909188
84580156166097919133875499200524063689912560717606
05886116467109405077541002256983155200055935729725
71636269561882670428252483600823257530420752963450
aby pokazać jak wykorzystać i co daje optymalizacja statyczna i dynamiczna podawana jako opcja do kompilatora g++.
Ok, pierw przedstawmy problem po polsku ;) Jest sobie dłuuugaaa liczba – 1000 znaków. A naszym zadaniem jest znalezienie największej wartości stworzonej podczas mnożenia 5 kolejnych cyfr tej liczby. Trudne się nie wydaje. Analizujemy to metodą brute force, czyli bierzemy 5 pierwszych cyfr, mnożymy je, zapamiętujemy, cofamy się o 4, bierzmy znów 5 cyfr i tak w kółko. Potem z tablicy, gdzie mamy zapamiętane wyniki, szukamy największej wartości. Przedstawię kod:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 | #include #include #include using namespace std; using std::string; int f(int* tt){ return tt[0]*tt[1]*tt[2]*tt[3]*tt[4]; //funkcja mnoży } int main(){ ifstream myfile; myfile.open ("p.txt");//plik z długą liczbą string a,line; if (myfile.is_open()) { while ( myfile.good() ) { getline (myfile,line); a.append(line);//odczytujemy po linii i wszystko do stringa } myfile.close(); } int tab[4]={0}; // tablica na pośrednie wartości int tabw[1000]={0}; // tablica na wyniki int y=0;// zmienne sterujące pętlą int il=0; for(int i=0;i<a.length();i++){//od początku do końca stringa if(il%5==0 and il!=0){//jeśli il się wypełni - liczymy wartość pośrednią, zapisujemy, zerujemy //zmienna odpowiedzialną za chodzenie po tablicy wartości posrednich //zwiększamy zmienną sterującą zapisem do tablicy wyników i cofamy się o 4. tabw[y]=f(tab); y++; il=0; i=i-4; } tab[il]=a.at(i)-48; // zapis do tablicy wartości pośrednich il++; } int max; max=tabw[0]; for(int r=0;r<1000;r++){ //tutaj szukamy już wartości największej if(tabw[r]>max) max=tabw[r]; cout<<tabw[r]<<endl; } cout<<"MAX: "<<max; return 0; } |
Nie sądzę żeby kod był jakoś bardzo zoptymalizowany. Ale działa – podaje poprawny wynik :)
Złożoność obliczeniowa na oko.. No to jedna pętla po całości, druga też… No jakieś ![]()
Sprawdźmy ile się ten kod wykonuje. A i kompiluję w ten sposób: g++ -Wall -g -pedantic test.cpp -o A
Wpisuję time ./A i dostaję:
1 2 3 | real 0m0.020s user 0m0.004s sys 0m0.008s |
Widać że kiepsko :P Ale za chwilę wpisuje to samo i dostaję inny wynik. I kolejny raz znów inny czas. Wezmę więc 10 czasów, pobieranych co około pół minuty, oto one:
1 2 3 4 5 6 7 8 9 10 | 020s 014s 022s 023s 020s 018s 021s 018s 019s 016s |
Spisywałem tylko wyniki z wiersza real. Czyli realny czas wykonania się programu. Uśredniając te czasy, przyjmujemy że czas potrzebny na wykonanie się programu to 019s.
Operacje optymalizacyjne, to takie przestawianie instrukcji dla procesora, aby unikać różnych konfliktów zasobów.
Aby włączyć optymalizację komendę dotyczącą kompilacji musimy wzbogacić o kolejny argument:
1 2 3 4 5 | g++ -Wall -g -O0 -pedantic test.cpp -o A // brak kompilacji g++ -Wall -g -O1 -pedantic test.cpp -o A // dla 1 stopnia optymalizacji g++ -Wall -g -O2 -pedantic test.cpp -o A // dla 2 stopnia optymalizacji g++ -Wall -g -O3 -pedantic test.cpp -o A // dla 3 stopnia optymalizacji g++ -Wall -g -Os -pedantic test.cpp -o A // nacisk na zmniejszenie rozmiaru kodu + flagi optymalizacyjne jak w poziomie 2 |
Ok, to sprawdźmy czas dla -O1 :) oto one:
1 2 3 4 5 6 7 8 9 10 | 015s 012s 009s 018s 017s 022s 021s 011s 021s 019s |
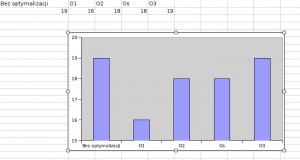
Zauważamy dość duży skok wydajności! Średnia z tych wyników to 016s
Teraz czas na -O2:
1 2 3 4 5 6 7 8 9 10 | 022s 012s 023s 020s 020s 005s 022s 019s 021s 019s |
Popatrz, prócz jednego czasu, reszta wydaje się być wolniejsza od optymalizacji na poziomie 1. Średnia to: 018s – wynik dość zaskakujący.
Czas na -O3:
1 2 3 4 5 6 7 8 9 10 | 022s 020s 012s 019s 019s 018s 012s 018s 021s 020s |
Średnia również 018s. Teraz -Os:
1 2 3 4 5 6 7 8 9 10 | 018s 020s 016s 019s 019s 023s 020s 018s 020s 022s |
Średania to 019s.
Skąd takie zachowanie przy O3? 3 poziom nie jest zalecanym poziomem optymalizacji. W znacznym stopniu modyfikuje kod wynikowy. W naszym przypadku najlepszym wyborem będzie 1 poziom optymalizacji.
Testy przeprowadzone na Lubuntu (lekka odmiana Ubuntu). Komputer: Laptop HP, 2GB pamięci i dwurdzeniowy procesor 1,8 GHz.
Mateusz Mazurek